2013年4月26日 星期五

2.1 the besection method 習題組 2.1 NO.5

Numerical Analysis數值分析筆記 / 2.1 The Bisection Method / 習題組 2.1 /

2.1 NO.05a_01
2.1 NO.05b_01
on 沒有留言:

2013年4月25日 星期四

2.1 the besection method 習題組 2.1 NO.4

Numerical Analysis數值分析筆記 /  

2.1 The Bisection Method / 

習題組 2.1 /


NO.4.
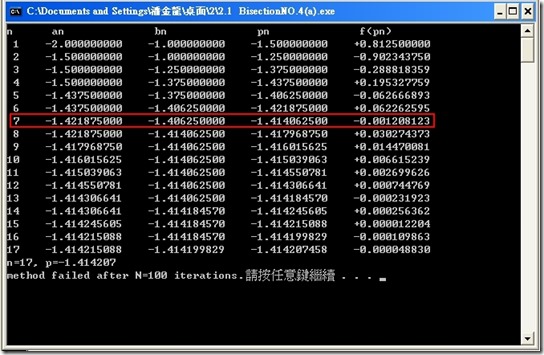
use the Bisection method to find solutions accurate to within $10^{-2}$ for $x^{4}-2x^{3}-4x^{2}+x+4=0$ on each interval.
  • 第01題 $\left[-2,\ -1\right]$
  • 第02題 $\left[0,\ 2\right]$
  • 第03題 $\left[2,\ 3\right]$
  • 第04題 $\left[-1,\ 0\right]$

>>第01題<< | 第02題 | 第03題 | 第04題

2.1 NO.04a_01
2.1 NO.04a_02
2.1 NO.04a_03
2.1 NO.04a_04


C 語言程式：


  1. #include <stdio.h>
  2. /*前置處理指命，就是把stdio.h這個檔案(此檔案附於安裝編譯器的子資料夾下)的內容放在原始程式的最開頭*/
  3. #include <stdlib.h>
  4. /*為了避免結果一閃而過(在windowXP系統下會出現此情形，均需加上此程式)*/
  5. #include <math.h>       /**/
  6. float f(float x);
  7. int main(void)
  8. { 
  9.     int i=0,N=100;
  10.     float a=-2,b=-1,p=0.0,FA=0.0,FP=0.0;
  11.     float TOL=0.00001;
  12.     printf("n      an              bn              pn              f(pn)\n");
  13.     /*Step1*/
  14.     i=1;
  15.     FA=f(a);
  16.     /*Step2*/
  17.     while(i<=N)
  18.     {    /*Step3*/
  19.          p=a+(b-a)/2;
  20.          FP=f(p);
  21.     printf("%2d    %+.9f    %+.9f    %+.9f    %+.9f\n",i,a,b,p,f(p));    
  22.          /*Step4*/
  23.          if(FP==0 || (b-a)/2<TOL)
  24.          {printf("n=%d, p=%+f\n",i,p);break;}
  25.          /*Step5*/
  26.          i=i+1;
  27.          /*Step6*/
  28.          if(FA*FP>0){a=p;FA=FP;}
  29.          else b=p;
  30.          }
  31.     printf("method failed after N=%d iterations.",N);
  32.     /*Step*/
  33.     /*Step*/
  34.     /*Step*/
  35. system("PAUSE"); /*為了避免結果一閃而過(在windowXP系統下會出現此情形，均需加上此程式)*/
  36. return 0;       
  37.    }
  38. float f(float x)
  39. {
  40.       return pow(x,4)-2*pow(x,3)-4*pow(x,2)+4*x+4;
  41.       }

C 語言程式執行結果： 


2.1 BisectionNO.4a


>>第01題<< | 第02題 | 第03題 | 第04題




on 沒有留言:

2013年4月24日 星期三

2.1 the besection method 習題組 2.1 NO.3

Numerical Analysis數值分析筆記 /  

2.1 The Bisection Method / 

習題組 2.1 /


NO. 3.
use the Bisection method to find solutions accurate to within $10^{-2}$ for $x^{3}-7x^{2}+14x-6=0$ on each interval.
  • 第01題 $\left[0,\ 1\right]$.
  • 第02題 $\left[1,\ 3.2\right]$.
  • 第03題 $\left[3.2,\ 44\right]$.

2.1 NO.03a_01

C語言程式：
  1. #include <stdio.h>
  2. /*前置處理指命，就是把stdio.h這個檔案(此檔案附於安裝編譯器的子資料夾下)的內容放在原始程式的最開頭*/
  3. #include <stdlib.h>
  4. /*為了避免結果一閃而過(在windowXP系統下會出現此情形，均需加上此程式)*/
  5. #include <math.h>       /**/
  6. float f(float x);
  7. int main(void)
  8. { 
  9.     int i=0,N=100;
  10.     float a=0,b=1,p=0.0,FA=0.0,FP=0.0;
  11.     float TOL=0.00001;
  12.     printf("n    an            bn            pn            f(pn)\n");
  13.     /*Step1*/
  14.     i=1;
  15.     FA=f(a);
  16.     /*Step2*/
  17.     while(i<=N)
  18.     {    /*Step3*/
  19.          p=a+(b-a)/2;
  20.          FP=f(p);
  21.     printf("%2d    %+.9f    %+.9f    %+.9f    %+.9f\n",i,a,b,p,f(p));    
  22.          /*Step4*/
  23.          if(FP==0 || (b-a)/2<TOL)
  24.          {printf("n=%d, p=%+f\n",i,p);break;}
  25.          /*Step5*/
  26.          i=i+1;
  27.          /*Step6*/
  28.          if(FA*FP>0){a=p;FA=FP;}
  29.          else b=p;
  30.          }
  31.     printf("method failed after N=%d iterations.",N);
  32.     /*Step*/
  33.     /*Step*/
  34.     /*Step*/
  35. system("PAUSE"); /*為了避免結果一閃而過(在windowXP系統下會出現此情形，均需加上此程式)*/
  36. return 0;       
  37.    }
  38. float f(float x)
  39. {
  40.       return pow(x,3)-7*pow(x,2)+14*x-6;
  41.       }

C語言程式執行結果：


2.1 BisectionNO.3a 

on 沒有留言:

2013年4月11日 星期四

2.1 the besection method 習題組 2.1 NO.2

Numerical Analysis數值分析筆記 / 2.1 The Bisection Method / 習題組 2.1 /



NO.2.
$f(x)=3(x+1)(x-\frac{1}{2})(x-1)$. Use the Bisection method on the following intervals to find $p_{3}$.
  • $\left[-2,\ 1.5\right]$
2.1 NO.02_012.1 NO.02_02

執行結果：

2.1 BisectionNO.2a 
  • $\left[-1.25,\ 2.5\right]$

2.1 NO.02_03

執行結果：
2.1 BisectionNO.2b

好像有算錯了^__^
on 沒有留言:

2.1 the besection method 習題組 2.1 NO.1

Numerical Analysis數值分析筆記 / 

2.1 The Bisection Method /

習題組 2.1 /



NO.1.
use the bisetion method to find the $p_3$ for $f(x)=\sqrt{x}-\cos x $ on $[0,1]$.


2.1 NO.01


C 程式語言：

    1. #include <stdio.h>
    2. #include <stdlib.h>
    3. #include <math.h>       /**/
    4. float f(float x);
    5. int sig(float v);
    6. int main(void)
    7. { 
    8.     int i=0,N=100;
    9.     float a=0.0,b=1.0,p=(a+b)/2,FA=0.0,FP=0.0;
    10.     float TOL=0.00001;
    11.    
    12.     printf("n  an         bn         pn         f(pn)\n");
    13.     /*Step1*/
    14.     i=1;
    15.     FA=f(a);
    16.    
    17.     /*Step2*/
    18.     while(i<=N)
    19.     {    /*Step3*/
    20.          p=a+(b-a)/2;
    21.          FP=f(p);
    22.         
    23.     printf("%2d  %.9f  %.9f  %.9f  %+.9f\n",i,a,b,p,f(p));    
    24.         
    25.          /*Step4*/
    26.          if(FP==0 || (b-a)/2<TOL)
    27.          {printf("n=%d, p=%+f\n",i,p);break;}
    28.         
    29.          /*Step5*/
    30.          i=i+1;
    31.         
    32.          /*Step6*/
    33.          if(sig(FA)*sig(FP)>0){a=p;FA=FP;}
    34.          else b=p;
    35.          }
    36.     printf("method failed after N=%d iterations.",N);
    37.    
    38.    
    39.    
    40. system("PAUSE");
    41. return 0;       
    42.    }
    43.   
    44.   
    45. float f(float x)
    46. {
    47.       return sqrt(x)-cos(x);
    48.       }
    49.      
    50. int sig(float u)
    51. {   
    52.      if(u>0){return 1;}
    53.      else if(u<0){return -1;}
    54.      else {return 0;}
    56.      }

    c語言執行結果：

     2.1 BisectionNO.1
    on 沒有留言:
    訂閱： 文章 (Atom)